Elephants

Memory limit: 64 MB

A parade of all elephants is to commence soon at the Byteotian zoo. The zoo employees have encouraged these enormous animals to form a single line, as the manager wills it to be the initial figure of the parade.

Unfortunately, the manager himself came to the parade and did not quite like what he saw - he had intended an entirely different order of the elephants. Therefore he enforced his ordering, claiming the animals would seem most majestic this way, and made the employees reorder the elephants accordingly.

As a pack of moving elephants can wreak havoc, the employees decided to have them rearranged by swapping one pair at a time. Luckily the animals need not stand next to each other in order to swap positions in the line. Making an elephant move, however, is not as easy as it sounds. In fact, the effort one has to put into it is proportional to the animal's mass. Hence, the effort involved in swapping a pair of elephants of respective masses 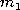and 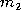can be estimated by 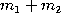. What is the minimum effort involved in rearranging the elephants according to manager's will?

Write a programme that:

• reads from the standard input the masses of all elephants from the zoo, along with their current and desired order in the line,
• determines a sequence of elephant swaps leading from the initial to the desired order of animals in the line, such that this sequence minimises the summary effort involved in all the swaps,
• prints out the summary effort on the standard output.

Input

The first line of the standard input contains a single integer (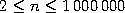) denoting the number of elephants in the zoo. We assume that the elephants are numbered from 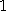to to simplify things. The second line holds integers 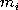( 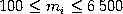dla 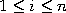) separated by single spaces and denoting the masses of respective elephants (in kilogrammes).

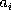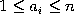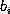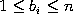The third line of input contains pairwise different integers () separated by single spaces and denoting the numbers of successive elephants in the initial ordering. The fourth line holds pairwise different integers () separated by single spaces and denoting the numbers of successive elephants in the ordering desired by the zoo manager. You may assume that the sequences 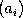and 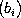differ.

Output

The first and only line of the standard output should contain a single integer denoting the minimum summary effort involved in reordering the elephants from the order represented by the sequence to the one represented by .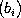

Example

For the input data:

6
2400 2000 1200 2400 1600 4000
1 4 5 3 6 2
5 3 2 4 6 1

the correct result is:

11200

One of the optimal rearrangements consists of swapping the following pairs of elephants:

• 2 and 5 - effort involved: 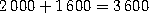, order achieved: 1 4 2 3 6 5,
• 3 i 4 - effort involved: 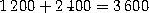, order achieved: 1 3 2 4 6 5,
• 1 i 5 - effort involv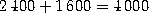ed: , order achieved: 5 3 2 4 6 1, which is the one desired.

Task authors: Jakub Radoszewski and Wojciech Rytter.